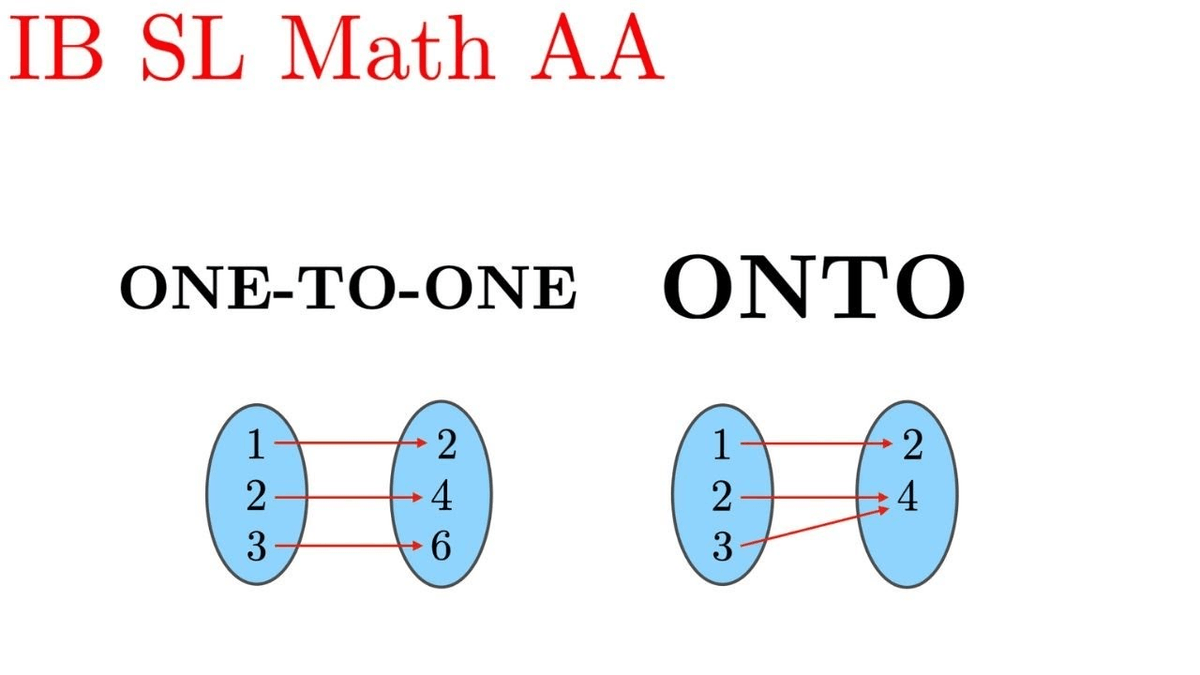
Sometimes we use illustrations to describe how one set maps to another in order to see if it is one-to-one. If the two outputs \(f(a)\), \(f(b)\) are different from each other (that is, not equal to each other) for all pairs \(a\) and \(b\), then the function is one-to-one. Select two values, \(a\) and \(b\), on the \(x\)-axis, and determine the \(y\)-values \(f(a)\) and \(f(b)\) that the function gives us at those two points. The formal method we use to show that a function is one-to-one is as follows:
One-to-One Sample Questions How to Determine if a Function is One-to-One